Subject: Mathematics (Basic)
Class X
Time Allowed: 3 hours
Max Marks: 80
General Instructions:
1. This Question Paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each
3. Section B has 5 questions carrying 02 marks each.
4. Section C has 6 questions carrying 03 marks each.
5. Section D has 4 questions carrying 05 marks each.
6. Section E has 3 case based integrated units of assessment (04 marks each) with sub-parts of the values of 1, 1 and 2 marks each respectively.
7. All Questions are compulsory. However, an internal choice in 2 Qs of 5 marks, 2 Qs of 3 marks and 2 Questions of 2 marks has been provided. An internal choice has been provided in the 2marks questions of Section E
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
SECTION A
Section A consists of 20 questions of 1 mark each.
1. If α and β are the zeroes of the polynomial 2x2 – 13x + 6, then α + β is equal to
(a) -3
(b) 3
(c) 13/2
(d) -13/2
2. The point on the x -axis which is equidistant from the points A (- 2, 3) and B (5, 4) is
(a) (0, 2)
(b) (2, 0)
(c) (3, 0)
(d) (- 2, 0)
3. The value of k for which the system of linear equations x + 2y = 3, 5x + ky + 7 = 0 is inconsistent is
(a) -14/3
(b) 2/5
(c) 5
(d) 10
4. The roots of the quadratic equation x2 – 0.04 = 0 are
(a) ±0.2
(b) ±0.02
(c) 0.4
(d) 2
5. A tree casts a shadow 15 m long on the level of ground, when the angle of elevation of the sun is 45c. The height of a tree is
(a) 10 m
(b) 14 m
(c) 8 m
(d) 15 m
6. A sector is cut from a circular sheet of radius 100 cm, the angle of the sector being 240c. If another circle of the area same as the sector is formed, then radius of the new circle is
(a) 79.5 cm
(b) 81.5 cm
(c) 83.4 cm
(d) 88.5 cm
7. The quadratic equation 2x2 – √5 x + 1 = 0 has
(a) two distinct real roots
(b) two equal real roots
(c) no real roots
(d) more than 2 real roots
8. If the common difference of an AP is 5, then what is a a18 – a13?
(a) 5
(b) 20
(c) 25
(d) 30
9. Δ ABC is an equilateral triangle with each side of length 2p. If AD ⊥ BC then the value of AD is
(a) √3
(b) √3 p
(c) 2p
(d) 4p
10. In figure, O is the centre of circle. PQ is a chord and PT is tangent at P which makes an angle of 50° with ∠POQ is
(a) 130°
(b) 90°
(c) 100°
(d) 75°
11. If cos (α + β) = 0, then sin (α – β) can be reduced to
(a) cosβ
(b) cos 2β
(c) sinα
(d) sin 2α
12. The base radii of a cone and a cylinder are equal. If their curved surface areas are also equal, then the ratio of the slant height of the cone to the height of the cylinder is
(a) 2 : 1
(b) 1 : 2
(c) 1 : 3
(d) 3 : 1
13. In a frequency distribution, the mid value of a class is 10 and the width of the class is 6. The lower limit of the class is
(a) 6
(b) 7
(c) 8
(d) 12
14. If a card is selected from a deck of 52 cards, then the probability of its being a red face card is
(a) 3/26
(b) 3/13
(c) 2/13
(d) ½
15. The point P on x -axis equidistant from the points A (-1, 0) and B (5, 0) is
(a) (2, 0)
(b) (0, 2)
(c) (3, 0)
(d) (-3, 5)
16. If one zero of the polynomial (3x2 + 8x + k) is the reciprocal of the other, then value of k is
(a) 3
(b) -3
(c) 1/3
(d) -1/3
17. If 3x + 4y : x + 2y = 9:4, then3x + 5y : 3x – y is equal to
(a) 4 : 1
(b) 1 : 4
(c) 7 : 1
(d) 1 : 7
18. The distance between the points (a cos θ + b sin θ, 0), and (0, a sin θ – b cos θ) is
(a) a2 + b2
(b) a2 – b2
(c) √ (a2 + b2)
(d) √ (a2 – b2)
19. Assertion: Sum of first 10 terms of the arithmetic progression -0.5, -1.0, -1.5, ………. is 31.
Reason: Sum of n terms of an AP is given as Sn = n/2[2a + (n – 1) d] where a is first term and d common difference.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true
20. Assertion: When a positive integer a is divided by 3, the values of remainder can be 0, 1 or 2.
Reason: According to Euclid’s Division Lemma a = bq + r, where 0 ≤ r < b and r is an integer.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true
Section – B
Section B consists of 5 questions of 2 marks each.
21. ABCD is a trapezium in which AB || CD and its diagonals intersect each other at the point O. Show that, AO/BO =CO/DO
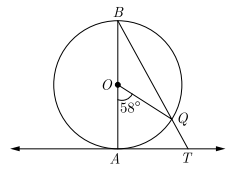
22. In given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58c, find ∠ATQ.
23. Find the value of cos 2θ, if 2 sin 2θ = √3.
24. Find the mean of the following distribution:

OR
Find the mean of the following data:

25. Show that 5√6 is an irrational number
OR
Write a rational number between √2 and √3.
Section – C
Section C consists of 6 questions of 3 marks each.
26.
27. If 1 + 3 sin2 θ = 3 sin θ cos θ, prove that tan θ = 1 or ½.
28. A horse is tethered to one corner of a rectangular field of dimensions 70 m x 52 m, by a rope of length 21 m. How much area of the field can it graze?
OR
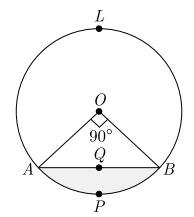
In the given figure, a chord AB of the circle with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (Use π = 3.14)
29. Find the mode of the following frequency distribution:

30. Find the ratio in which the segment joining the points (1, -3) and (4, 5) is divided by x -axis? Also find the coordinates of this point on x -axis.
OR
The vertices of ΔABC are A (6, -2), B (0, -6) and C (4, 8). Find the co-ordinates of mid-points of AB, BC and AC.
31. Write the smallest number which is divisible by both 306 and 657.
Section – D
Section D consists of 4 questions of 5 marks each
32. Determine graphically the coordinates of the vertices of triangle, the equations of whose sides are given by 2y – x = 8, 5y – x = 14 and y – 2x = 1.
OR
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the co-ordinates of the vertices of the triangle formed by these lines and the X-axis and shade the triangular region.
33. Two tangents PA and PB are drawn from an external point P to a circle with centre O, such that ∠APB = ∠x and ∠AOB = ∠y. Prove that opposite angles are supplementary.
34. The person standing on the bank of river observes that the angle of elevation of the top of a tree standing on opposite bank is 60°. When he moves 30 m away from the bank, he finds the angle of elevation to be 30°. Find the height of tree and width of the river.
OR
As observed from the top of a 100 m high light house from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the light house, find the distance between the two ships [Use √3 = 1.732]
35. A hemispherical depression is cut from one face of a cubical block, such that diameter l of hemisphere is equal to the edge of cube. Find the surface area of the remaining solid.
Section – E
Case study based questions are compulsory.
36. Maximum Profit: A kitchen utensils manufacturer can produce up to 200 utensils per day. The profit made from the sale of these utensils can be modelled by the function P(x) = -0.5x + 175x – 330, where P(x) is the profit in Rupees, and x is the number of utensils made and sold. Based on this model,
(i) Find the y -intercept and explain what it means in this context.
(ii) Find the x -intercepts and explain what they mean in this context.
(iii) How many utensils should be sold to maximize profit?
OR
What is the maximum profit?

37. Tania is very intelligent in math’s. She always try to relate the concept of math’s in daily life. One day she plans to cross a river and want to know how far it is to the other side. She takes measurements on her side of the river and make the drawing as shown below.
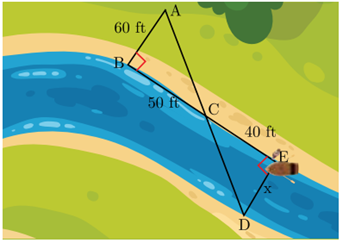
(i) Which similarity criterion is used in solving the above problem?
(ii) Consider the following statement:
S1: ∠ACB = ∠DCE
S2: ∠BAC = ∠CDE
Which of the above statement is/are correct.
(a) S1 and S2 both
(b) S1
(c) S2
(d) None
(iii) Consider the following statement:
S3: AB/DE = CA/CD
S4: BC/CE = AB/DE
S5: CA/CD = DE/AB
Which of the above statements are correct ?
(a) S3 and S5
(b) S4 and S5
(c) S3 and S4
(d) All three
(iv) What is the distance x across the river?
OR
What is the approximate length of AD shown in the figure?
38. Double-six Dominos: It is a game played with the 28 numbered tiles shown in the diagram.

The 28 dominos are placed in a bag, shuffled, and then one domino is randomly drawn. Give the following answer.
(i) What is the probability the total number of dots on the domino is three or less?
(ii) What is the probability the total number of dots on the domino is greater than three?
(iii) What is the probability the total number of dots on the domino does not have a blank half?
OR
What is the probability the total number of dots on the domino is not a “double” (both sides the same)?